[zh-CN] Cryptonote whitepaper

目前仅仅包括部分内容, 有翻译不准确或者错误的地方欢迎到 这里提 Issue 指正

4.2 Definitions (定义)

4.2.1 Elliptic curve parameters (椭圆曲线参数)

As our base signature algorithm we chose to use the fast scheme EdDSA, which is developed and implemented by D.J. Bernstein et al. [18]. Like Bitcoin’s ECDSA it is based on the elliptic curve discrete logarithm problem, so our scheme could also be applied to Bitcoin in future.

作为基础签名算法, 我们选择使用 EdDSA(Edwards-curve Digital Signature Algorithm 爱德华兹曲线数字签名算法) 和 Bitcoin 的 ECDSA (椭圆曲线数字签名算法)一样, EdDSA 也是基于 椭圆曲线离散对数问题, 所以未来 比特币也可以使用 Cryptonote 方案 : )

Common parameters are:

公共参数如下:

• $q$ : 一个质数; a prime number; $q$ = $ 2^{255} $−19;
• $d$ : Fq 的一个元素an element of $F_q$ ; $d$ = −121665/121666;
• $E$ : 椭圆曲线方程 an elliptic curve equation; $-x^2 + y^2 = 1 + dx^2y^2$
• $G$ : 一个基点(位于座标轴上); a base point; $G=(x,-4/5)$
• $l$ : 基点的素数阶 a prime order of the base point; $l= 2^{252} + 27742317777372353535851937790883648493;$
• $H_s$ : 哈希函数 a cryptographic hash function ${0,1}^∗ \rightarrow F_q $;
• $H_p$ : 确定性哈希函数 a deterministic hash function $E(F_q) \rightarrow E(F_q )$.

4.2.2 Terminology (术语)

Enhanced privacy requires a new terminology which should not be confused with Bitcoin entities.

下面会定义一些新的属于, 从而避免和 Bitcoin 的用词相混淆.

private ec-key is a standard elliptic curve private key: a number $a \in [1,l-1] $

public ec-key is a standard elliptic curve public key: a point $A = aG$;

one-time key-air is a pair of private and public ec-keys;

private user key is a pair (a,b) of two different private ec-keys;

tracking key is a pair (a,B) of private and public ec-key ( where $B=bG $ and $a b$ )

public user key is a pair (A,B) of two public ec-keys derived from (a,b);

standard address is a representation of a public user key given into human friendly string with error correction;

trucated address is a representation of the second half (point B) of a public user key given into human friendly string with error correction.

私有 ec 密钥 (private ec-key) 是一个 标准的 椭圆曲线 私钥 : 数字 $a \in [1,l-1] $

公开 ec 密钥 (public ec-key) 是一个 标准椭圆曲线公钥: 一个点 $A = aG$

一次性密钥对 (one-time keypair) 是 一个 基于 椭圆曲线 的 公钥和私钥对

用户的私钥 (private user key) 是一个 用 两个不同的椭圆曲线 生成的密钥对 (a,b), 可以理解成 两个私钥,

追踪 密钥 (tracking key) 是 由 a 的私钥 和 b 公钥组成的密钥对 (a,B),当 $B = bG $ 并且 $a \neq b$

用户的公钥 (public user key) 是 由 用户的 私钥对(a,b) 派生出的 公钥对 (A,B)

标准地址 (standard address) 是 公开 用户的公钥 (A,B) 的 表示形式, 提供给人类友好的展示形式 并 带有错误纠正功能

具体地址 (trucated address) 是 公开 用户的密钥的后半部分 (B) 的表示形式, 提供给人类友好的展示形式 并 带有错误纠正功能

The transaction structure remains similar to the structure in Bitcoin: every user can choose several independent incoming payments (transactions outputs), sign them with the corresponding private keys and send them to different destinations.

交易结构和 Bitcoin 类似, 每个用户都可以将几个独立的 UTXO 作为输入, 使用对应私钥进行签名, 然后发送到不同的地址上.

Contrary to Bitcoin’s model, where a user possesses unique private and public key, in the proposed model a sender generates a one-time public key based on the recipient’s address and some random data. In this sense, an incoming transaction for the same recipient is sent to a one-time public key (not directly to a unique address) and only the recipient can recover the corresponding private part to redeem his funds (using his unique private key). The recipient can spend the funds using a ring signature, keeping his ownership and actual spending anonymous. The details of the protocol are explained in the next subsections.

Bitcoin 的模型中, 用户拥有唯一的私钥和公钥, 而在当前模式中, 发件人根据 收件人的地址 和 一些随机数据 生成 一次性公钥(one-time keypair). 从这个意义上说, 同一个收件人的交易将发送到 一次性公钥 上 (而不是直接发送到唯一的地址上), 只有收件人 可以使用相应的私钥来从一次性公钥上赎回他的资金. 收款人可以使用 环签名机制来消费这笔资产, 这样 收款人就可以在保证其对 这笔资产 的所有权的情况下 保障了实际交易的匿名性. 协议的详细内容将在接下来的小节中解释.

4.3 Unlinkable payments (无法连接的交易们)

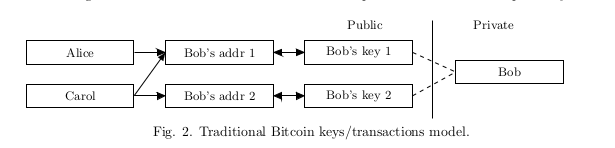
Classic Bitcoin addresses, once being published, become unambiguous identifier for incoming payments, linking them together and tying to the recipient’s pseudonyms. If someone wants to receive an “untied” transaction, he should convey his address to the sender by a private channel. If he wants to receive different transactions which cannot be proven to belong to the same owner he should generate all the different addresses and never publish them in his own pseudonym.

在经典的 Bitcoin 网络中, 收款地址一旦公布, 那么就会成为一个明确的标识, 会将这个收款地址和使用者联系起来, 并且计算出通过这个收款地址 转入和转出的资产列表. 如果有人想接受匿名的交易, 那么他应该通过私人渠道将 自己的地址 告诉发件人. 如果他想接受 无法被证明属于同一个所有者的多个交易, 那么他需要生成不同的 Bitcoin 收款地址, 或者永远不要公布这个私人收款地址, 以防止 被和这个私人收款地址关联起来.

We propose a solution allowing a user to publish a single address and receive unconditional unlinkable payments. The destination of each CryptoNote output (by default) is a public key, derived from recipient’s address and sender’s random data. The main advantage against Bitcoin is that every destination key is unique by default (unless the sender uses the same data for each of his transactions to the same recipient). Hence, there is no such issue as “address reuse” by design and no observer can determine if any transactions were sent to a specific address or link two addresses together.

我们提出了一个解决方案, 允许用户发布一个单一的收款地址, 也可以做到 接受无法被追踪的转账.

每个 CryptoNote 的输出的 默认收款地址是一个 公共的密钥. 从真正的收款人的地址 和 发件人的随机数据 中计算得到. 这个方案对于 Bitcoin 的优势在于, 每个 公共密钥 也就是 一次性密钥 的 的地址都是唯一的 (除非 发送者 对同一个 收款人的每笔交易都使用相同的数据). 因此, 在设计上就不存在 “地址重用” 这个问题. 任何的观察者都无法确定 , 是否有任何交易被发送到特定的地址, 或者 将两个交易联系在一起.

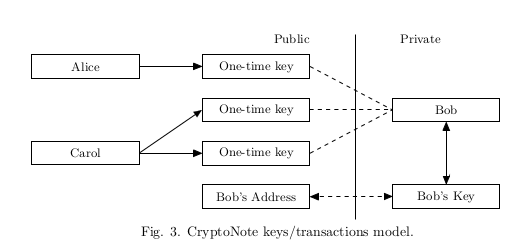
First, the sender performs a Diffie-Hellman exchange to get a shared secret from his data and half of the recipient’s address. Then he computes a one-time destination key, using the shared secret and the second half of the address. Two different ec-keys are required from the recipient for these two steps, so a standard CryptoNote address is nearly twice as large as a Bitcoin wallet address. The receiver also performs a Diffie-Hellman exchange to recover the corresponding secret key.

首先, 发送者进行 Diffie-Hellman 交换 , 通过可信的方式, 得到 收款者的 一些用于生成 一次性密钥 的信息 和 接受者的一半的地址(例如, 只给私钥中的后半段 B 点.) . 然后 发送者 使用 信息 和 后半段地址, 计算出一个一次性目的的密钥. 这两步需要收件人提供他的 (A,B) 公钥. 所以一个标准 CryptoNote 的长度 几乎是 Bitcoin 钱包地址 的两倍. 然后 收款者 还要进行 Diffie-Hellman 交换 来恢复相应的密钥.

A standard transaction sequence goes as follows:

一个标准的交易流程如下:

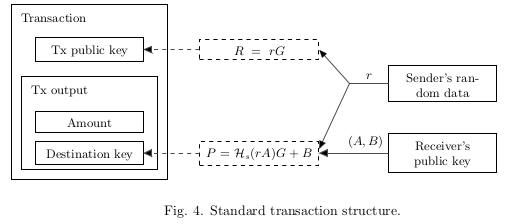
1. Alice wants to send a payment to Bob, who has published his standard address. She unpacks the address and gets Bob’s public key (A, B).
2. Alice generates a random $r \in [1, l−1]$ and computes a one-time public key $P=H_s(rA)G+B$.
3. Alice uses $P$ as a destination key for the output and also packs value $R = rG$ (as a part of the Diffie-Hellman exchange) somewhere into the transaction. Note that she can create other outputs with unique public keys: different recipients’ keys ($A_i , B_i $) imply different $P_i$ even with the same $r$.

1. Alice 想要给 Bob 发一笔钱, Bob 已经公布了自己的 标准地址(基于 Bob 的 (A,B) 的人类友好的表示形式) , Alice 解开地址, 得到了 Bob 的公钥对 (A,B).
2. Alice 生成了一个随机的 $r$ ( $r \in [1, l−1]$ )(你可以把 r 看成一个基于 椭圆曲线 生成的私钥) , 并且计算了一个一次性密钥 $P$ ($P=H_s(rA)G+B$ )
3. Alice 使用 一次性密钥 $P$ 作为输出目的的密钥, 并且在交易报文的某个地方, 打包一个 $R$ ( $R=rG$ ) (你可以把 R 看成是 r 的公钥), 用来作为 Diffie-Hellman 交换 的一部分. 请注意, Alice 可以使用 同样的 $R$ 来创建别的交易输出. 即便是相同的 $R$, 不同的接受者密钥 $(A_i,B_i)$ 也意味着不同的 $P_i$.

4. Alice sends the transaction.
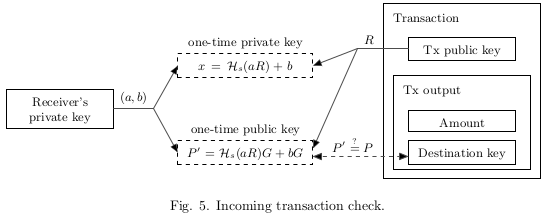
5. Bob checks every passing transaction with his private key $(a, b)$, and computes $P’ = H_s(aR)G+B$. If Alice’s transaction for with Bob as the recipient was among them, then $aR = arG = rA$ and $P’ = P$ .
6. Bob can recover the corresponding one-time private key: $x = H_s (aR) + b$, so as $P = xG$. He can spend this output at any time by signing a transaction with $x$.

4. Alice 发送了一笔交易 到一次性密钥
5. Bob 用它的私钥 $(a,b)$ 检查每笔通过的交易, 并计算 $P’ = H_s(aR)G+B$. 如果检查到 发送给 Bob 的 交易, 并且 $aR = arG = rA$ and $P’ = P$ .
6. Bob 可以使用他的用户私钥, 来恢复相应的一次性密钥 : $x = H_s (aR) + b$, 得到 $P=xG$ . 他可以在任何时候用 $x$ 签署一个 交易来花费这笔 UTXO.

As a result Bob gets incoming payments, associated with one-time public keys which are unlinkable for a spectator. Some additional notes:

结果 Bob 得到了 这笔转入资金. 由于这个一次性公钥仅仅使用一次, 所以这个这笔交易对 旁观者来说是无法连接的, 无法推断出这笔交易的双方. 除了上面信息之外, 这里还有一些附加说明

• When Bob “recognizes” his transactions (see step 5) he practically uses only half of his private information: $(a, B)$. This pair, also known as the tracking key, can be passed to a third party (Carol). Bob can delegate her the processing of new transactions. Bob doesn’t need to explicitly trust Carol, because she can’t recover the one-time secret key $p$ without Bob’s full private key $(a, b)$. This approach is useful when Bob lacks bandwidth or computation power (smartphones, hardware wallets etc.).
• In case Alice wants to prove she sent a transaction to Bob’s address she can either disclose $r$ or use any kind of zero-knowledge protocol to prove she knows $r$ (for example by signing the transaction with $r$).
• If Bob wants to have an audit compatible address where all incoming transaction are linkable, he can either publish his tracking key or use a truncated address. That address represent only one public ec-key $B$, and the remaining part required by the protocol is derived from it as follows: $a=H_s(B)$ and $A=H_s(B)G$. In both cases every person is able to “recognize” all of Bob’s incoming transaction, but, of course, none can spend the funds enclosed within them without the secret key b.

• 当 Bob “识别” 他的交易的时候(见上述 第五步 $P’ = H_s(aR)G+B$), 这里Bob 只用了 a 的私钥和 b的公钥 ($a,B$), $(a,B)$ 通常称为 跟踪密钥, 可以传递给第三方(例如 Carol). Bob 可以将新的交易委托给 Carol. Bob 不需要明确的信任 Carol, 因为如果没有 Bob 的完整密钥 $(a,b)$, 那么 Carol 就无法恢复一次性密钥 $P$, 当 Bob 缺乏 带宽 或者 计算能力 的时候(智能手机, 硬件钱包等), 这种方法很有用.
• 如果 Alice 想证明 她向 Bob 的地址发送了一笔交易, Alice 可以公开 $r$, 或者使用任何一种零知识证明协议来证明 Alice 知道 $r$ (例如用 $r$ 签署交易)
• 如果 Bob 想拥有一个 可以被审计的地址, 所有的 传入交易都是可以链接的. 那么他可以发布 他的 跟踪密钥 $(a,B)$ ,或者 一个截断的地址 B, 协议所需的其他部分由 B 派生, $a=H_s(B)$ and $A=H_s(B)G$. 但是, 由于没有密钥 b, 所以谁也不能花掉其中的资金.

4.4 One-time ring signatures (一次性环签名)

A protocol based on one-time ring signatures allows users to achieve unconditional unlinkability. Unfortunately, ordinary types of cryptographic signatures permit to trace transactions to their respective senders and receivers. Our solution to this deficiency lies in using a different signature type than those currently used in electronic cash systems.

基于 一次性 环签名 的协议, 允许 用户实现无法追踪的转账. 但比较遗憾的是, 普通类型的加密签名允许跟踪交易到其各自的发送者和接收者. 我们使用与电子现金系统(ECS) 中当前使用的签名类型不同的签名类型 来解决这个问题

We will first provide a general description of our algorithm with no explicit reference to electronic cash.

首先我们先对 算法进行一般性描述, 而不提及电子现金系统.

A one-time ring signature contains four algorithms: (GEN, SIG, VER, LNK):

• GEN: takes public parameters and outputs an ec-pair $(P, x)$ and a public key $I$.
• SIG: takes a message m, a set $S’$ of public keys ${P_i}_{i\neq s}$ , a pair $(P_s , x_s)$ and outputs a signature $σ$ and a set $S = S’ ∪ {P_s }$.
• VER: takes a message m, a set S, a signature σ and outputs “true” or “false”.
• LNK: takes a set $I = {I i }$, a signature $σ$ and outputs “linked” or “indep”.

一次性环签名包含四种算法: (GEN, SIG, VER, LNK):

• GEN: 接受公共参数 然后 输出 密钥对 $(P,x)$ 和 公钥 $I$
• SIG: 接受如下参数, 输出签名 $σ$ 和 一组 $S = S’ ∪ {P_s }$
  • 一个信息 m
  • 一组 关于 $S’$ 的公钥 ${P_i}_{i\neq s}$
  • 以及一对 $(P_s , x_s)$
• VER: 接受 一个信息 m, 一组 S , 一个签名 σ , 输出 “True” 或者 “False”
• LNK: 接受一对 $I$=${I_i}$, 一个 签名 σ, 然后输出 “linked” or “indep”

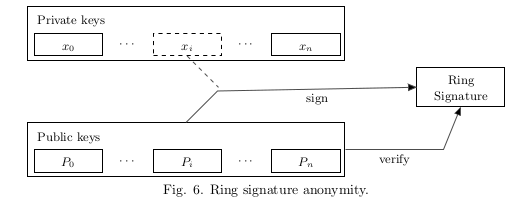
The idea behind the protocol is fairly simple: a user produces a signature which can be checked by a set of public keys rather than a unique public key. The identity of the signer is indistinguishable from the other users whose public keys are in the set until the owner produces a second signature using the same keypair.

这个协议背后的想法很简单, 用户产生一个签名，可以通过一组公共密钥而不是唯一的公共密钥来检查该签名. 签字人的身份与公钥就在这一组公钥中, 其他用户无法区分. 但如果 签名者使用相同的公钥来进行第二个签名的话, 那么就可以找到签名者身份和所使用的密钥.

• GEN: The signer picks a random secret key $ x ∈ [1, l − 1] $and computes the corresponding public key $P = xG$. Additionally he computes another public key $I = xH_p (P )$ which we will call the “key image”.
• SIG: The signer generates a one-time ring signature with a non-interactive zero-knowledge proof using the techniques from $[21]$. He selects a random subset $S’$ of $n$ from the other users’ public keys $P_i$ , his own keypair $(x, P)$ and key image $I$. Let $0 ≤ s ≤ n $ be signer’s secret index in $S$ (so that his public key is $P_s$ ).

• Gen: 签名者选择一个随机私钥 $ x ∈ [1, l − 1] $ 并计算相应的公钥 $P=xG$. 此外, 他还计算了另一个公钥 $I = xH_p (P )$, 我们将这个密钥称为 Key Image
• SIG: 签名者生成 无交互 零知识证明的 一次性环形签名. 他从 其他用户用户的公钥集合 $P_i$ 以及他自己的密钥对 $(x,P)$ 和 Key Image 中, 选择 $n$ 个随机子集 $S’$, 并让 他子集的公钥包含在这些子集中. (他自己的公钥是 $P_s$, s 是在子集中的次序 )

He picks a random ${q_i | i = 0 . . . n} $ and ${w_i | i = 0 . . . n, i \neq s}$ from $(1 . . . l)$ and applies the following transformations: $$ L_i=\begin{cases} q_iG & \text{if } i = s; \ q_iG + w_iP_i, & \text{if } i \neq s \ \end{cases} \ R_i=\begin{cases} q_iH_p(P_i), & \text{if } i =s \ q_iH_p(P_i) + w_iI, & \text{if } i \neq s\ \end{cases} $$

The next step is getting the non-interactive challenge: $$ c = H_s (m, L _1 , . . . , L_n , R_1 , . . . , R_n ) $$

Finally the signer computes the response:

$$ c_i=\begin{cases} w_i && \text{if } i \neq s; \ c - \sum_{i=0}^n c_i & mod \space l, & \text{if } i = s \ \end{cases} \ r_i=\begin{cases} q_i && \text{if } i \neq s; \ q_s - c_sx & mod \space l, & \text{if } i = s \ \end{cases} $$

The resulting signature is $ σ = (I, c_1 , . . . , c_n , r_1 , . . . , r_n )$.

VER: The verifier checks the signature by applying the inverse transformations: $$ \begin{cases} L_i^\prime = r_iG + c_iP_i \ R_i^\prime = r_iH_p(P_i)+c_iI \end{cases} $$

Finally, the verifier checks if $$ \sum_{i=1}^{n} c_i \overset{?}{=} H_s(m,L_0^\prime…..,L_n^\prime,R_0^\prime…..R_n^\prime) \ mod \ \ l $$ If this equality is correct, the verifier runs the algorithm LNK. Otherwise the verifier rejects the signature. LNK: The verifier checks if I has been used in past signatures (these values are stored in the set L ). Multiple uses imply that two signatures were produced under the same secret key. The meaning of the protocol: by applying L-transformations the signer proves that he knows such x that at least one $P_i = xG$. To make this proof non-repeatable we introduce the key image as $I = xH_p (P )$. The signer uses the same coefficients $(r_i , c_i )$ to prove almost the same statement: he knows such x that at least one $H_p (P_i ) = I · x^−1$ . If the mapping $x → I$ is an injection:

1. Nobody can recover the public key from the key image and identify the signer;
2. The signer cannot make two signatures with different I’s and the same $x$.

A full security analysis is provided in Appendix A.

他选择了 一个随机的 $q_i$, 这个 i 大于0 小于 n, 以及一个 $w_i$, 这个 i 也大于 0 小于 n , 同时不等于 s.并且 应用如下转换

$$ L_i=\begin{cases} q_iG & \text{if } i = s; \ q_iG + w_iP_i, & \text{if } i \neq s \ \end{cases} \ R_i=\begin{cases} q_iH_p(P_i), & \text{if } i =s \ q_iH_p(P_i) + w_iI, & \text{if } i \neq s\ \end{cases} $$

下一步是应对非交互的挑战:

$$ c = H_s (m, L _1 , . . . , L_n , R_1 , . . . , R_n ) $$

最后, signer 完成如下 response:

$$ c_i=\begin{cases} w_i && \text{if } i \neq s; \ c - \sum_{i=0}^n c_i & mod \space l, & \text{if } i = s \ \end{cases} \ r_i=\begin{cases} q_i && \text{if } i \neq s; \ q_s - c_sx & mod \space l, & \text{if } i = s \ \end{cases} $$

生成的签名是 $ σ = (I, c_1 , . . . , c_n , r_1 , . . . , r_n )$.

VER: 验证者通过应用逆变换来检查签名:

$$ \begin{cases} L_i^\prime = r_iG + c_iP_i \ R_i^\prime = r_iH_p(P_i)+c_iI \end{cases} $$

最后, 验证者检查

$$ \sum_{i=1}^{n} c_i \overset{?}{=} H_s(m,L_0^\prime…..,L_n^\prime,R_0^\prime…..R_n^\prime) \ mod \ \ l $$

如果此等式正确, 那么验证程序将运行算法 LNK. 否则, 验证者将拒绝签名.

LNK: 验证者 检查是否在过去的签名中使用过 $I$ (这些值存储在 $L$ 中).多次使用意味者两个签名是在同一个 私钥下产生的.

协议的含义: 通过应用 L 变换, 签名者证明他知道 $x$, 至少有一个 $P_i = xG$. 为了使该证明不可重复, 我们将 key image 引入为 $I = xH_p (P )$. 签名人 使用相同的系数 $(r_i , c_i )$, 证明 来证明, 他知道 x 至少有一个 $H_p (P_i ) = I · x^−1$ .

如果 $x → I$ 这个映射是注入:

1. 没有人可以从 key image 中恢复 公钥 并 识别签名者
2. 签名人不能使用不同的 $I$ 和相同的 $ x $ 进行两个签名。

在附录A 中提供了完整的安全性分析.

4.5 Standard CryptoNote transaction (标准 CryptoNote 转账)

By combining both methods (unlinkable public keys and untraceable ring signature) Bob achieves new level of privacy in comparison with the original Bitcoin scheme. It requires him to store only one private key (a, b) and publish (A, B) to start receiving and sending anonymous transactions.

通过结合两种方法 (不可关联的 公钥 和 不可追踪的 环签名), 与原始的 Bitcoin 方案相比, Bob 实现了更高的隐私级别. 这个方案要求 Bob 仅仅存储一对私钥 (a,b) 并发布一对公钥(A,B), 以开始接受和发布匿名交易.

While validating each transaction Bob additionally performs only two elliptic curve multi-plications and one addition per output to check if a transaction belongs to him. For his every output Bob recovers a one-time keypair $(p_i , P_i )$ and stores it in his wallet. Any inputs can be circumstantially proved to have the same owner only if they appear in a single transaction. In fact this relationship is much harder to establish due to the one-time ring signature.

在验证每笔交易的同时, Bob 还执行两次 椭圆曲线乘法 和 每项输出一次 加法, 用以检查某笔交易是否属于他. 对于 他的每个输出, Bob 恢复一次性密钥对 $(p_i , P_i )$ 并将其存储在他的钱包中. 仅当 Output 出现在单个事务中时, 才能明确证明任何输入都具有相同的所有者. 实际上，由于一次性的环签名，这种关系很难建立。

With a ring signature Bob can effectively hide every input among somebody else’s; all possible spenders will be equiprobable, even the previous owner (Alice) has no more information than any observer.

有了环签名，Bob 可以有效地将他的每一个交易隐藏在无数的交易当中 .所有人对于 Bob 是否发起了这笔交易都是一无所知,甚至之前的所有者（Alice）的信息也不比任何观察者多.

When signing his transaction Bob specifies n foreign outputs with the same amount as his output, mixing all of them without the participation of other users. Bob himself (as well as anybody else) does not know if any of these payments have been spent: an output can be used in thousands of signatures as an ambiguity factor and never as a target of hiding. The double spend check occurs in the LNK phase when checking against the used key images set.

在签署交易时, Bob 指定了 n 个与输出相同的无关输出, 在没有任何其他用户参与的情况下, 混合了这些输出. Bob 本人(以及其他任何人) 都不知道这些 UTXO 是否已经用尽. 输出结果可以可以用于成千上万的签名. 对于已经使用的 Key Image 进行检查时, 双花检查将会在 LNK 阶段进行.

Bob can choose the ambiguity degree on his own: n = 1 means that the probability he has spent the output is 50% probability, n = 99 gives 1%. The size of the resulting signature increases linearly as $O(n + 1)$, so the improved anonymity costs to Bob extra transaction fees. He also can set n = 0 and make his ring signature to consist of only one element, however this will instantly reveal him as a spender.

Bob 可以子集选择歧义读, 如果 n=1, 那么表示 他花费 Output 的概率是 50%, n=99 表示 1%. 生成签名的大小随着 $O(n+1)$ 线性增加, 因此匿名性的提升时 Bob 付出了额外的交易费用. 他还可以设置 n=0 并使他的 环签名仅仅包含一个元素, 但是这将立刻显示出他是一个消费者.